Consider ‘s’ be the sources of monochromatic light wave ‘S1‘ and ‘S2‘ are the two coherent sources emitted from single point ‘s’ . Initially, the wave emitted from S1 and S2 are in phase but when they meet at point ‘p’ they are not in phase. Let be the phase difference of wave emitting from S1 and S2 and meeting at p and y1 and y2 be the displacement of wave emitting from S1 and S2 then,
According to the superposition principle,
The resultant displacement of the wave at p is given by,
This is the resultant wave equation at point ‘p’.
Squaring and adding equation (i) and (ii) we get,
Combining (iii) & (iv) relations, we get,
The intensity will be maximum
i.e. point ‘p’ will be the position of maximum intensity if phase difference of web emitting from s1 and s2 and meeting at point ‘p ‘is even integral multiple of p.
Similarly the point ‘p’ will be the position of minimum intensity,
So that point ‘p’ will be the position of minimum intensity if phase difference of wave emitted from S1 and S2 and meeting at ‘p’ is odd integral of p.

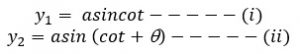
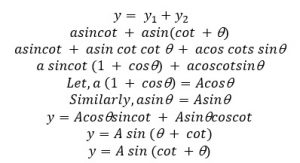
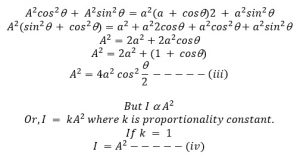
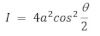
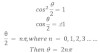
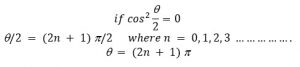

Top comments (0)