If two sides of a parallelogram are represented by two vectors A and B, then the magnitude of their cross product will be equal to the area of parallelogram i.e.
Proof
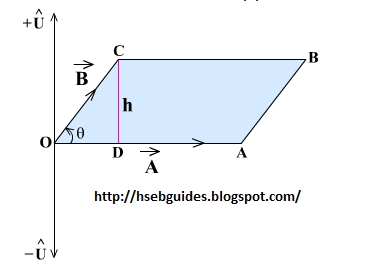
Consider a parallelogram OABC whose two sides are represented by two vectors A and B as shown. The area of parallelogram OABC is equal to:
D = hA—————-(1)
Draw perpendicular CD on side OA.
Consider right angled triangle COD
sinq = h/OCh= OC sinq h= B sinq
Putting the value of h in equation (1), we get,
D = B sinq AD = AB sinq


Top comments (0)