Properties of vector addition
Commutative law of vector addition
Consider two vectors
and
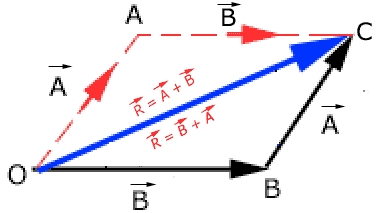
Let these two vectors represent two adjacent sides of a parallelogram. We construct a parallelogram OACB as shown in the diagram. The diagonal OC represents the resultant vector
Commutative law of vector addition
From above figure it is clear that:
This fact is referred to as the commutative law of vector addition.
Associative law of vector addition
The law states that the sum of vectors remains same irrespective of their order or grouping in which they are arranged.
Consider three vectors:
Applying “head to tail rule” to obtain the resultant of:
Then finally again find the resultant of these three vectors :
This fact is known as the associative law of vector addition.

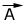
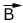
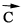



Top comments (0)