Volumetric expansion
Increase in volume of a body on heating is referred to as
Volumetric expansion or cubical expansion.
Consider a metallic body of volume = V1. Let it’s temperature is raised by T. Then experimentally “Increase in volume (V) is directly proportional to its initial volume (V1) and rise in temperature (T).
Where
is constant known as “coefficient of volumetric expansion”
Expression for final volume
We know that
Final volume = Initial volume + increase in volume
Coefficient of volumetric expansion
Coefficient of volumetric expansion is defined as:
“Increase in volume per unit original volume per Kelvin rise in temperature is called coefficient of volumetric expansion.”
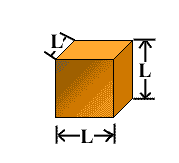
Consider a metallic cube of each side of length of “L”.
Before heating at T1 K
Volume of cube at T1 K :
V1 = L3 ———- 1
[V = L.B.H]
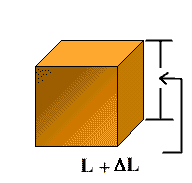
If it is heated to T2 K, then the length of each side will become (L + D L) and its volume will become
V2 = (L + D L) 3
since V2= V1 + D V
comparing above two equations
V1 + D V = (L + D L)3
as [ D L = a L D T ]
V1 + D V = (L + a L D T)3
V1 + D V = L3 (1 + a D T)3
Using formula [(a+b)3 = a3 + b3 + 3a2b + 3ab2]
V1 + D V = L3 {1 + a 3D T3 + 3(1)( a D T) + 3(1)( a 2 D T2)}
V1 + D V = L3 {1 + a 3D T3 + 3a D T + 3a 2 D T2}
Since “a ” is a fractional value of range 10-5 or 10-6, therefore we can neglect all the terms containing high powers of “a ” thus.
V1 + D V = L3 (1 + 3a D T)Putting the value of DV
V1 + b V1D T = V1 (1 + 3a D T) Since
[D V = V1b D T and L3 = V1]
This expression shows that the coefficient of the cubical expansion is three times of the coefficient of the linear expansion.

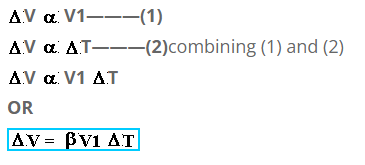
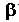
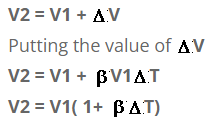
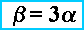
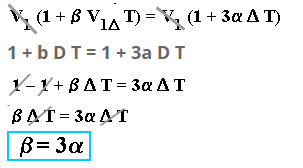

Top comments (0)