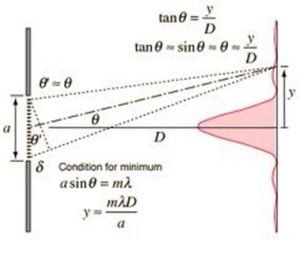
Consider a plane wave front incidents on the slit of width ‘d’. The light passing through the slit will converge by converging lens on screen which is at a distance ‘D’ from the slit. According to rectilinear propagation of light, it is expected that, the central bright spot at ‘o’ and there is dark on either side of ‘o’. But it is found that, there is central bright spot at ‘o’ and alternatively dark and bright fringes on either side of ‘o’. This is due to the diffraction of light at slit AB.
It is observed that, the intensity of central maxima is maximum and intensity of secondary maxima decreases as the distance from the central maxima increases. The width of central maxima is double, than that of secondary maxim.
Position of central maxima
If the light from the slit will converge at ‘o’, since the incident wave at AB is in phase, and they travel equal distance to converge the light at ‘o’. Hence the position of ‘o’ is always maximum intensity.
Position of secondary maxima and minima
Consider light wave will travel by inclination ‘o’ with initial direction and converge at ‘p’. Although the incident wave on slit are in phases, but they travel on converging at ‘p’ travel unequal distances. Hence the point ‘p’ will be position of maximum & minimum intensity, which depends upon the path difference of wave converging at ‘p’. The path difference of the wave emitting from A & B and meeting at p is given by,
BN = dsinθ
The point ‘p’ will be the position of secondary minima of path difference of wave emitting from A and B and meeting at p is integral multiple of 1
i.e. dsinθ = nλ where nλ= 1, 2, 3, …………………………
Similarly, the point ‘p’ will be the position of secondary minima of path difference of wave emitting from A and B and meeting at p is integral multiple of
i.e. dsinθ= nλ
Similarly, the point ‘p’ will be the position of secondary maxima if path difference of the wave emitting from A and B and meeting at p is odd integral multiple of 2.
i.e. dsinθ= (2n + 1) λ/2, n = 0, 1, 2, 3, ……………………..
Width of Central Maxima
If ‘p be the position of nth minima, then path difference,
dsinθ = nd
for nth minima since θ is very small, then Sinθ ≈ θ
If yn be the distance of nth maxima from the centre of fringe,
The difference of consecutive distances from the center of diffractive gives the width of secondary maxima
Since, width of central maxima is double then that secondary maxima,

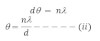
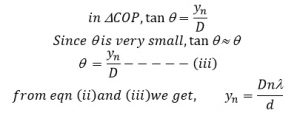

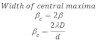

Top comments (0)