Inclined plane
Any plane surface which makes an angle q with the horizontal surface is called inclined plane such that0<q <90. . Inclined plane is an example of simple machine which is used to lift heavy bodies without applying very huge force.
Motion of a body on an inclined plane
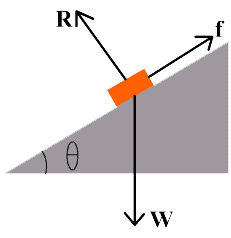
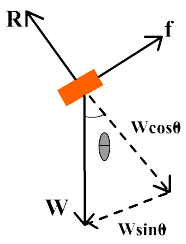
Consider a block of mass “m” placed on an inclined plane, which makes an angle q with the horizontal plane. The weight “W” of the block is acting vertically downward. The weight of the block can be resolved into two rectangular components: wcosq and wsinq
other forces acting on the block are:
- Surface reaction (R) which is perpendicular to the plane
- Force of friction (f) acting opposite to the direction of motion of block.
Let us take x-axis perpendicular to the inclined plane. If the block is at rest, then wsinq acting down the plane balances the opposing frictional force.
Applying 1st condition of equilibrium.
Fx = 0
f – wsinq = 0 ——-(1)
Fy = 0
R– wcosq = 0 ——-(2)
Since there is no motion in the direction perpendicular to the inclined plane, therefore wcosq is balanced by R i.e. R = wcosq
If block slides down with an acceleration equal to ‘a’, then the resultant force is equal to ‘ma’ and the force on block will be:
wsinq – f
According to 2nd law of motion
wsinq – f = ma
If the force of friction is negligible, then
wsinq = ma
but w = mg
This expression shows that if friction is negligible the acceleration of a body on an inclined plane is independent of mass but is directly proportional to sinq.
When friction is not negligible
1. If block moves upward
f – wsinq = ma
2. If block moves downward
wsinq – f = ma
Mechanical advantage of inclined plane
Mechanical advantage of inclined plane is given by
M.A = 1/sinq
Particular cases
1. When q = 0
a = g sin0
a = g x 0
a = o
2. When q = 30
a = g sin30
a = g x 0.5
a = g/2
a = 4.9 m/s2
3. When q = 60
a = g sin60
a = g x 0.866
a = 4.9 m/s2
4. When q = 90
a = g sin90
a = g x 1
a = g
a = 9.8 m/s2
Above analysis shows that the acceleration of a body on an inclined plane depends upon the angle of inclination.

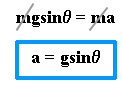

Top comments (0)