Law Of Conservation Of Energy

According to the law of conservation of energy :
“Energy can neither be created nor it is destroyed, however energy can be converted from one form energy to any other form of energy”

Show that the motion of a simple pendulum is according to the law of conservation energy
Or
Prove the law of conservation with the help of a suitable example.

We know that the motion of the bob of a simple pendulum is simple harmonic motion. Here we have to prove that the energy is conversed during the motion of pendulum.
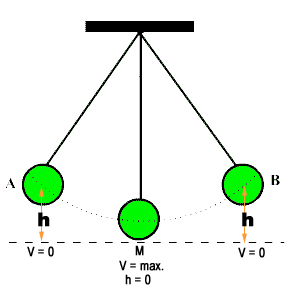
Proof: Consider a simple pendulum as shown in the diagram.

Energy conservation at point ‘A’
At point ‘A’ velocity of the bob of simple pendulum is zero. Therefore, K.E. at point ‘A’ = 0. Since the bob is at a height (h), Therefore, P.E. of the bob will be maximum. i.e.
P.E. = mgh.
Energy total = K.E. + P.E
Energy total = 0 + mgh
Energy total = mgh
This shows that at point A total energy is potential energy.

Energy conservation at point ‘M’
If we release the bob of pendulum from point ‘A’, velocity of bob gradually increases, but the height of bob will decreases from point to the point. At point ‘M’ velocity will become maximum and the height will be nearly equal to zero.
Thus ,
K.E. = maximum = 1/2mV2 but P.E. = 0.
Energy total = K.E. + P.E
Energy total = 1/2mV2 + 0
Energy total = 1/2mV2
This shows that the P.E. at point is completely converted into K.E. at point ‘M’.

Energy conservation at point ‘B’
At point M the bob of Pendulum will not stop but due to inertia, the bob will moves toward the point ‘B’. As the bob moves from ‘M’ to ‘B’, its velocity gradually decreases but the height increases. At point ‘B’ velocity of the bob will become zero.
Thus, K.E. at point ‘B’ = 0 but P.E. = max.
P.E. = mgh.
Energy total = K.E. + P.E.
Energy total = 0 + mgh
Energy total = mgh
This shows that at point B total energy is again potential energy.

Conclusion
Above analysis indicates that the total energy during the motion does not change. I.e. the motion of the bob of simple pendulum is according to the law of conservation of energy.