Show that the motion of a mass attached to the end of a spring is SHM
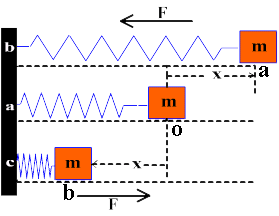
Consider a mass “m” attached to the end of an elastic spring. The other end of the spring is fixed at the firm support as shown in figure “a“. The whole system is placed on a smooth horizontal surface.
If we displace the mass ‘m‘ from its mean position ‘O‘ to point “a” by applying an external force, it is displaced by ‘+x‘ to its right, there will be elastic restring force on the mass equal to F on the left side which is applied by the spring.
According to “Hook’s Law
F = – Kx —- (1)
Negative sign indicates that the elastic restoring force is opposite to the displacement.
Where K= Spring Constant
If we release mass ‘m‘ at point ‘a‘, it moves forward to ‘ O‘. At point ‘ O‘ it will not stop but moves forward towards point “b” due to inertia and covers the same displacement –x. At point ‘b‘ once again elastic restoring force ‘F‘ acts upon it but now on the right side. In this way it continues its motion
from a to b and then b to a.
According to Newton’s 2nd law of motion, force ‘F‘ produces acceleration ‘a‘ in the body which is given by
F = ma —- (2)
Comparing equation (1) & (2)
ma = -kx
Here k/m is constant term, therefore ,
a = – (Constant)x
or
a a -x
This relation indicates that the acceleration of body attached to the end elastic spring is directly proportional to its displacement. Therefore, its motion is Simple Harmonic Motion.

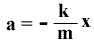

Top comments (0)