Motion Of A Projection Along It’s Diameter Is SHM

Figure 1

A particle is moving along a circular path with constant angular speed. Prove that the motion of its projection along one of its diameter is simple harmonic motion.
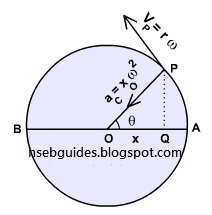
Consider a particle ‘P‘ moving around a circle of radius ‘r‘ ( r = xo) with uniform angular velocity ‘w‘. The linear speed of the particle is VP = xo w
From point ‘P‘ draw perpendicular PQ on AB. Point ‘Q‘ represents the projection of particle ‘P‘. When point ‘P‘ revolves around the circle, its projection ‘Q‘ oscillates to and fro along the diameter. When ‘P‘ ia at A or B, the displacement of ‘Q‘ becomes maximum i.e.
[Figure 1]
As ‘Q‘ moves away from equilibrium position ‘O‘, its velocity decreases and becomes zero at extreme points. When it moves towards ‘O‘ , its velocity increases from zero to maximum value. This shows that the acceleration of projection is proportional to its displacement and is directed to equilibrium position.
Hence, the motion of projection is simple harmonic motion.
MATHEMATICAL PROOF
Since ‘P‘ is moving along the circular path, its acceleration ia equal to centripetal acceleration
which is directed towards the centre of circle.
aP=ac
aP=mV2/r
aP= r w2
Since r = xO
aP= xOw2
The acceleration of the projection ‘aQ‘ is equal to the component of acceleration of particle ‘P‘ along the diameter AB
Since the acceleration of the projection is directly proportional to its displacement and always directed to mean position, therefore the motion of the projection of a particle moving around a circle with constant speed is simple harmonic in nature.