Simple pendulum
Simple pendulum consists of a heavy mass particle suspended by a light, flexible and in-extensible string.
Motion of a bob in a simple pendulum
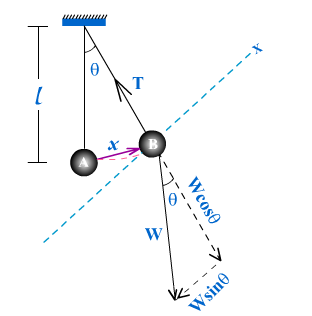
The motion of the bob of simple pendulum simple harmonic motion if it is given small displacement. In order to prove this fact consider a simple pendulum having a bob of mass ‘m‘ and the length of pendulum is ‘l‘. Assuming that the mass of the string of pendulum is negligible. When the pendulum is at rest at position ‘A‘, the only force acting is its weight and tension in the string. When it is displaced from its mean position to another new position say ‘B‘ and released, it vibrates to and fro around its mean position.
Suppose that at this instant the bob is at point ‘B‘ as shown above (FIG2)
Forces acting on the bob
- Weight of the bob (W) acting vertically downward.
- Tension in the string (T) acting along the string.
The weight of the bob can be resolved into two rectangular components:
- Wcosq along the string.
- Wsinq perpendicular to string.
Since there is no motion along the string, therefore, the component Wcosq must balance tension (T)
i.e. Wcosq = T
This shows that only Wsinq is the net force which is responsible for the acceleration in the bob of pendulum.
According to Newton’s second law of motion Wsinq will be equal to m x a
i.e. Wsinq = m a
Since Wsinq is towards the mean position, therefore, it must have a negative sign.
i.e. m a = – Wsinq
But W = mg
m a = – mgsinq
a = – gsinq
In our assumption q is very small because displacement is small, in this condition we can take sinq = q
Hence, a = – gq ———– (1)
If x be the linear displacement of the bob from its mean position, then from figure, the length of arc AB is nearly equal to x
From elementary geometry we know that:
Where s= x, r = l
Putting the value of q in equation (1)
As the acceleration of the bob of simple pendulum is directly proportional to displacement and is directed towards the mean position, therefore the motion of the bob is simple harmonic when it is given a small displacement.

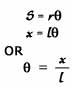


Top comments (0)