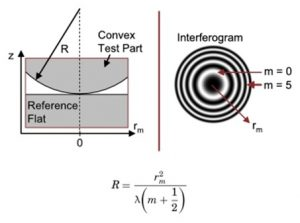
When a plano-convex lens is placed over a flat glass plate, then a thin air layer is formed between glass plate and a convex lens. If the radius of curvature of plano-convex lens is much greater than distance ‘r’ and the system is viewed through the above, the pattern of dark & bright ring is observed. This is called Newton’s Ring.
Theory:
Let ‘R’ be the radius of curvature of lens AOB and ‘C’ be the center of curvature, which is placed on a glass plate MON such that its surface just touches at point ‘o;. The circle AOBE is completed such that OOCE is its diameter.
The perpendicular AM and BN is drawn to glass plate such that AM =BN=t. Where ‘t’ is the thickness of air film.
When the light incidents on the air film, some parts of light is reflected from the upper surface and some parts of light is reflected from the lower surface of air film. The two beam of reflected light super impose to each other giving rise to interference.
The path difference is given by 2lt Cosθ, where ‘t’ is the thickness of the air film. U is refractive index of air film and r is the angle of reflection in air film.
As one of light suffer the phase angle change λ. Then total path difference is:
For maximum intensity,
For minimum intensity,
Form fig,
For bright fringe
If ‘r’ be the radius of nth bright fringe
To determine the wave length of monochromatic light:
If ‘l’ be the wave length of sodium light and rn be the radius of nth dark ring. Then diameter of nth dark ring.


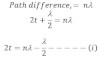
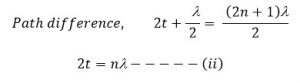
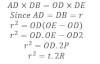




Top comments (0)