Aim: To determine refractive index of the material of the given prism by the method of i-d curve.
Apparatus:
- Drawing board
- Prism
- Drawing pins
- Needle point steel pins
- Drawing sheet
- Scale, set square ,protractor and a sharp pencil
Principle: When the prism is at minimum deviation position “Angle of incidence angle{i} = Angle of emergence angle{e} i.e (angle{i}= angle{e}) and the angle of refractions at both the surfaces of the prism will be equal i.e angle{r_1}= angle{r_2}. From geometry we have
d=i+e-A ; {r_1}+{r_2}= A
but when the prism is in minimum deviation d=D_m ,
D_m=2i-A since angle{i}= angle{e}
implies2i = A+D_m
implies i = frac{A+D_m}{2} – – – – – – – – – – – – (a)
and 2r =A since angle{r_1}= angle{r_2}= angle{r}
impliesr = frac{A}{2} – – – – – – – – – – – – (b)
But according to snell’s law mu= frac{Sini}{Sinr}
substituting the values of i and r in the above equation from equations (a) and (b) we get
mu= frac{sinfrac{(A+D_m)}{2}}{sin frac{A}{2}}
Theory: If the angle of the prism is angle{A} then angle of deviation angle{D} = angle{i}+angle{e}-angle{A} and angle{r_1}+angle{r_2}= angle{A}
If angle{A} is the angle of the prism,angle{D_m} the angle of minimum deviation.
Then the refractive index of the material of the prism mu= frac{sinfrac{(A+D_m)}{2}}{sin frac{A}{2}}
Procedure: We can divide the entire procedure of this experiment in to two parts:
- we have to first determine the angle of the prism A then
- We have to determine the angle of minimum deviation D of the prism.
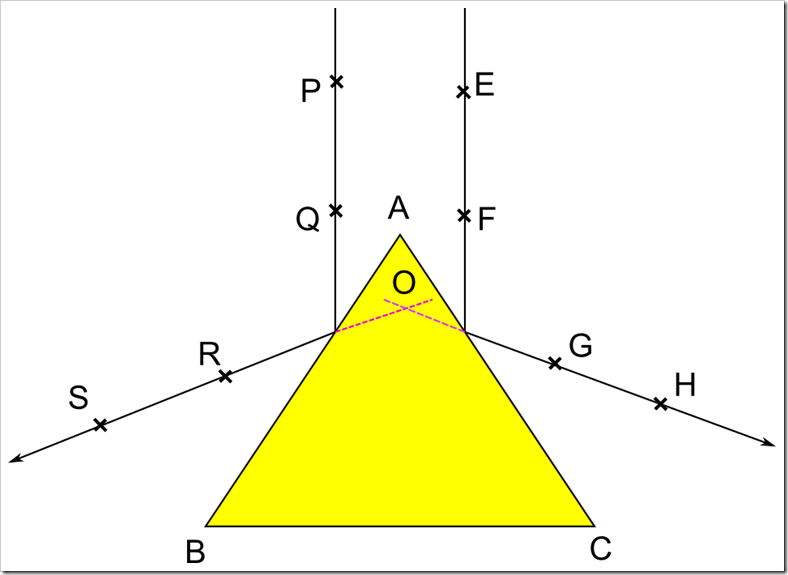
Part 1: Determine the angle of the prism A:Place the drawing board on the table and fix the drawing sheet on the drawing board using drawing pins. P lace the prism on the drawing sheet, holding the prism trace the outer boundary of the prism which will be triangle .Mark the three vertices of the triangle as A,B and C. Now draw two parallel lines so that the edge A lies symmetrically between parallel lines.
Then two pins are fixed on one of the lines at points P and Q. Looking through the face AB two more pins are fixed at the points R and S so that the reflective images of the pins at P an Q lie in the same straight line with these two pins without any parallax error. Now join the points R and S using a scale .The RS line represents the reflected ray of PQ. In the same way repeat the procedure on the other face of the prism AC, to get the reflected images G,H of the incident ray passing through EF. Remove the prism and extend the st.lines passing through RS and GH in to triangle ABC so that they meet at a point O.
Measure the angle ROG which will be equal to 2A
Hence angle{A} = frac{angle{ROG}}{2}
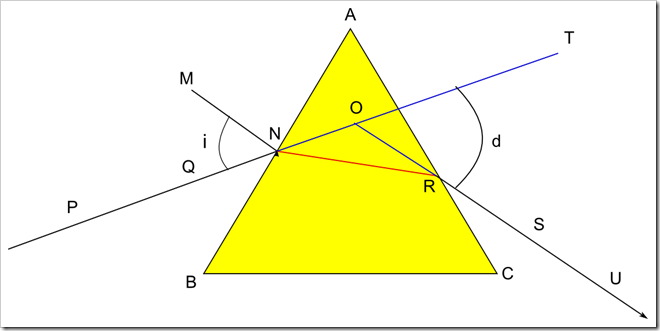
Part 2: Determine the angle of minimum deviation angle{D_m}:Fix the drawing sheet on the drawing board using drawing pins, keep the prism on the paper and trace the prism. The trace will give us a triangle ABC.
AB reflecting surface , AC refracting surface and BC is the base of the prism.Draw a normal line MN to the reflecting surface at N.Draw a incident line PQ making some angle (>30degrees) with the normal line MN.Now place the prism on its trace along ABC.Fix two pins on the incident ray at two points P and Q .Now observing through the face AC two pins S and U are fixed so that these two pins at S and U will be in the line with P and Q.Remove the prism join the points S and U with a st line which meets the face AC at R.Extend the incident ray PQ forward and emergent ray SU backwards till the meet at O.
Measure the angle{TOR}=d.
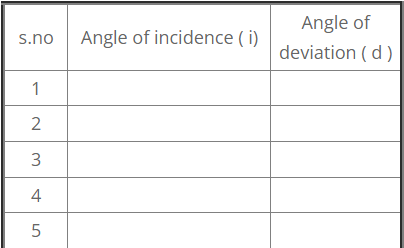
repeat the experiment in the above said procedure for various angles of incidences i.e 35,40,45,50,55 ……. and measure the respective angles of deviations d1,d2,d3,d4,d5….. record these values in the table.
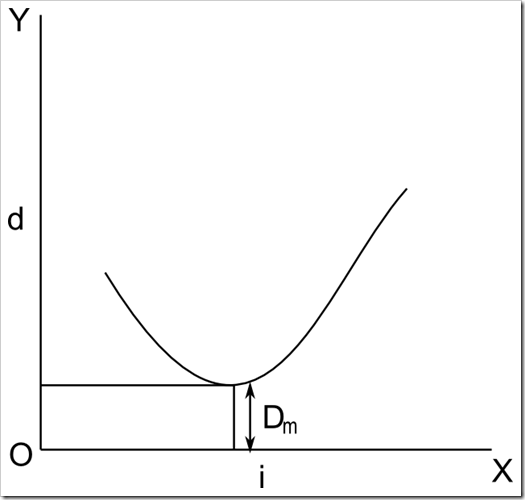
i-d curve: Now draw a graph taking the angles of incidences(i) on X-axis and the angles of deviations(d) on the Y-axis.join these points with a smooth curve which will be a parabola.
From the graph the angle of minimum deviation can be calculated.
Observations:
- Angle of the prism A =
- Angle of minimum deviation D_m = ( from graph) substituting the values of the angle of prism A and the angle of minimum deviation D_m in the formula of refractive index mu= frac{sinfrac{(A+D_m)}{2}}{sin frac{A}{2}}, we can calculate the refractive index of the material of the prism.
Precautions:
- Pins should be fixed perfectly vertical
- While fixing the pins in line with the refractive or reflective images of incident rays care should be taken for the parallax error.
- There should be some space between the pins
- Pins should not be disturbed during the experiment
- Same edge of the prism should be taken as vertex A for all the observations
- Clean both the faces AB and AC of the prism proper before taking the readings.
Result: Refractive index of the material of the prism

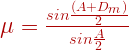
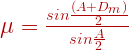

Top comments (0)