The tension is defined as:
“The force exerted by a string when it is subjected to pull”.
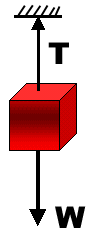
If a person is holding a block of weight W attached to the end of a string, a force is experienced by him. This force is known as Tension. When the body is at rest, the magnitude of tension is equal to the weight of the body suspended by the string. Tension and the weight acts in the opposite direction. Tension is vector quantity, which has both magnitude and direction. Its magnitude remains constant at all points of the string.
Unit of tension
Since tension is a force, therefore, it has same units as that of force. In S.I. system : NEWTON In C.G.S. system : DYNE In F.P.S. system : pound
Motion of bodies connected by a string
When the bodies move vertically
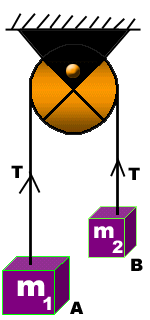
Consider two bodies of unequal masses m1 and m2 connected by the ends of a string, which passes over a frictionless pulley as shown in the diagram.
If m1>m2, the body ‘A’ will move downward with acceleration ‘a’ and the body ‘B’ will move up with same acceleration. Here we have to find the value of ‘a’ and tension ‘T’.
Forces acting on body A
There are two forces acting on A:
- Weight of body: w1 = m1g
- Tension in the string = T
The net force acting on the body is
F= m1g – T
Net force acting on body ‘A’ is given by Newton’s 2nd law as m1a. Thus, we have the equation for the motion of body “A” as:
m1g – T = m1a ——— (1)
Forces acting upon body B
There are also two forces acting on B:
- Weight of body: w2 = m2g
- Tension in the string = T
Since body “B” is moving up, the net force acting on body is
F= T – m2g
T – m2g = m2a———- (2)
Adding (1) & (2)
putting the value of ‘a’ in equation (2) to find the magnitude of

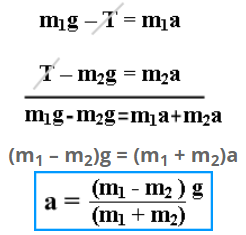
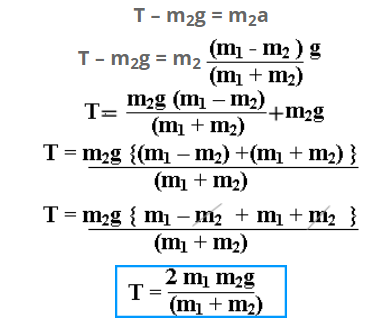

Top comments (0)