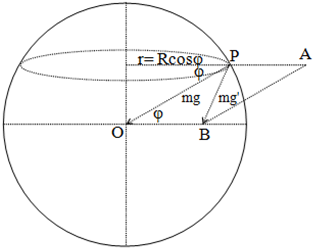
Let us consider the earth to be a spherical ball of mass ‘M’ and radius ‘R’. An object of mass ‘m’ is at point P at latitude φ, when the earth is not rotating the weight of the object is mg. But earth is rotating with angular velocity ω. So, the object is moving in a circular path of radius ‘r’ as shown in the figure. The object experiences centrifugal force,
The object is being acted by two forces ‘mg’ and ‘Ff‘. The resultant of these two forces gives the apparent weight of the object (m’g). The resultant of the two forces is given by the diagonal of the parallelogram OPAB.
From parallelogram law of vector addition:
The value of ω is in the order of 10-4. So, the term containing ω-4is much smaller than 1 and ω2so can be neglected.
So, acceleration due to gravity is minimum at the equator.
At poles; φ = 90°
g’ = g
So, acceleration due to gravity is maximum at poles.
Hence, acceleration due to gravity decreases due to rotation while it increases due to increase in latitude.

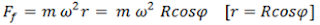
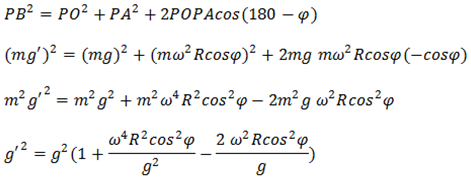


Top comments (0)