When a string of mass per unit length (m) under the action of tension; T; is set in to transverse vibration the velocity of the wave propagation through the string is given by
m = tm
In such a vibration of the string the disturbance produced at one fixed end. Travels along the string and gets reflected back at the other end, since the original wave and reflect wave have the same frequency and amplitude, they superimpose to produce stationary transverse wave.
Different modes of Vibration in stretched string:
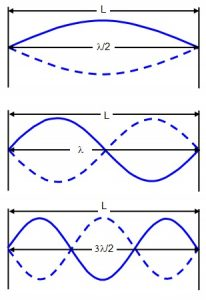
1. First mode of vibration:
In this mode of vibration, the string vibration in one segment. This there are two nods at fixed ends and an antinode in between them. If ‘λ’ be the length of string and λ0 be the wave length of wave in this mode of vibration.
If ‘U’ be the velocity of wave and to be the frequency of wave in this mode of vibration
This is the fundamental frequency or frequency of 1st harmonics.
2. Second mode of vibration:
In this mode of vibration the string vibration in two segments. Thus there are three nodes and two antinodes between of string and l1 be the wavelength of wave in this mode of vibration.
l = λ1
If u be the velocity of wave and f1 be the frequency of wave in this mode of vibration.
This is the frequency of 1st overtone and 2nd harmonics.
3. Third mode of vibration:
4 nodes & 3 AN
This is the frequency of 2nd overtone or 3rd harmonics
In this way, for the 4th, 5th …… modes of vibration in the stretched string the frequency.
For the fifth, 5th….. Harmonics are emitted.
The general equation of frequency of wave in stretched string is given by,
Laws of transverse vibration of a string:

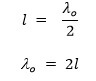

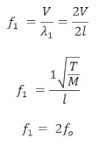
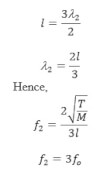
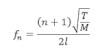
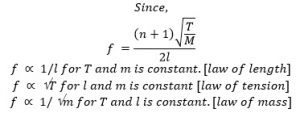

Top comments (0)