Introduction to rectangular component method
Rectangular component method of addition of vectors is the simplest method to add a number of vectors acting in different directions.
Details of method
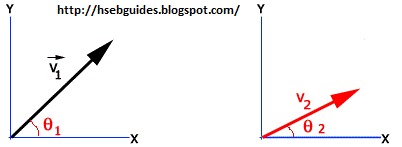
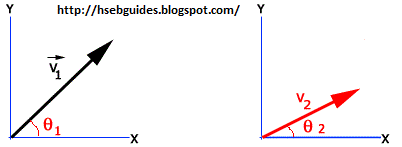
Consider two vectors:
making angles q1 and q2 with +ve x-axis respectively.
Step 1:
Step 2:
Step 3:
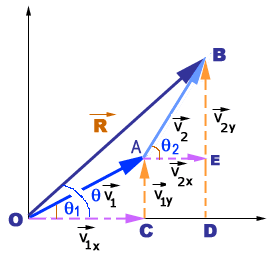
Representative lines of v1 and v2 are OA and OB respectively. Join O and B which is equal to resultant vector of v1 and v2.
Step 4:
Resultant vector along X-axis can be determined as:
Step 5:
Resultant vector along Y-axis can be determined as:
Step 6:
Now we will determine the magnitude of resultant vector.
In the right angled triangle DBOD:
Step 7:
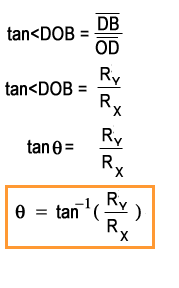
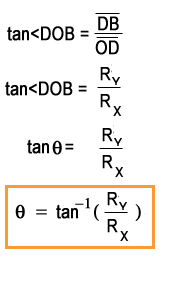
Finally, the direction of resultant vector will be determined.
Again in the right angled triangle DBOD:
Where q is the angle that the resultant vector makes with the positive X-axis.
In this way we can add a number of vectors in a very easy manner.
This method is known as addition of vectors by rectangular components method.






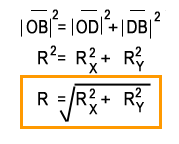

Top comments (0)