Gaseous molecules are in continuous motion. They collide with each other and with the walls of the container. When they collide with the walls of the container, they transfer an amount of their momentum to the walls. Since a number of molecules collide the walls of the container, therefore the walls of the container are constantly under the influence of the force. This force expressed per unit area is called gas pressure.
Mathematically,
P = F/A
Expression for gas pressure
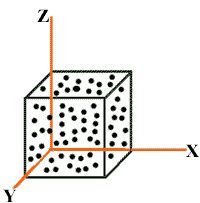
Consider “N” molecules of a gas enclosed in a cubical container of each side equal to “L”.
Mass of each molecule is “m”.
Area of each wall = A = L2
Volume of container = V = L3
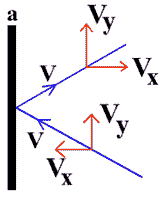
Consider the motion of those molecules moving along x- axis towards the wall marked “a”.
Taking the example of a molecule moving from right to left . Velocity of molecule along x-axis is equal to vx
Initial momentum of the molecule = m x – vx = -mvx
Final momentum of the molecule = mvx
Change in momentum = mvx – (-mvx)
Change in momentum = mvx + mvx
D M = 2mvx…………(a)
time taken for one collision
s = v t
t = s/v…………(b)
in one collision distance covered is ,
s = 2L
v = vx
Putting the values of v and s in equation (b)
t = 2L/vx
But rate of change of momentum is equal to the applied force.
F = mvx2/L
Thus the total force on the wall “a”
F = F1 + F2 + F3 + —————— + Fn
F = mv1x2/L + mv2x2/L + mv3x2/L + —————— + mvnx2/L
F = m/L(v1x2 + v2x2 + v3x2 + —————— + vnx2 )
Multiply and dividing by N on R.H.S.


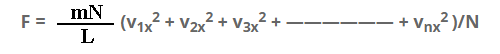


Top comments (0)