The law of conservation of angular momentum states that:
“When the net external torque acting on a system about a given axis is zero, the total angular momentum of the system about that axis remains constant.”
Mathematically
Proof
According to the second law of motion net force acting on a body is equal to its rate of change of linear momentum.
i.e.
Differentiating both sides with respect to "t"
Which is the required equation.
This expression states that the torque acting on a particle is the time rate of change of its angular momentum. If the net external torque on the particle is zero, then,
Or,
Thus the angular momentum of a particle is conserved if and only if the net external torque acting on a particle is zero.


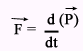

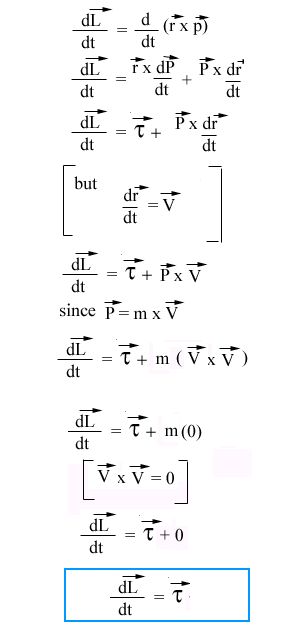
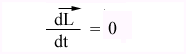


Top comments (0)