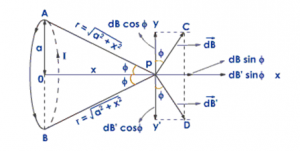
Consider a circular coil having radius a and centre O from which current I flows in anticlockwise direction. The coil is placed at YZ plane so that the centre of the coil coincide along X-axis. P be the any point at a distance x from the centre of the coil where we have to calculate the magnetic field. let dl be the small current carrying element at any point A at a distance r from the point P where
the angle between r and dl is 90°. Then fron biot-savart law, the magnetic field due to current carrying element dl is:
The direction of magnetic field is perpendicular to the plane containing dl and r. So the magnetic field dB has two components:
Similarly, consider another current carrying element dl’ which is diametrically opposite to the point A. The magnetic field due to this current carrying element dB’ also has two components:
Here both dBcosθ and dB’cosθ are equal in magnitude and opposite in direction. So they cancel each other. Similarly, the components dBsinθ and dB’sinθ are equal in magnitude and in same direction so they adds up.
Total magnetic field due to the circular current carrying coil at the axis is:
This is the expression for magnetic field due to circular current carrying coil along its axis.
If the coil having N number of turns then magnetic field along its axis is:

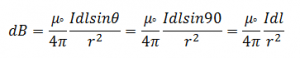



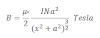

Top comments (0)