MOLAR SPECIFIC HEAT AT CONSTANT PRESSURE Content
MOLAR SPECIFIC HEAT AT CONSTANT PRESSURE
|
MOLAR SPECIFIC HEAT AT CONSTANT PRESSURE
|
||
|
“The a mount of heat energy required to raise the temperature of one mole of a gas
by one Kelvin at constant pressure is called molar specific heat at constant pressure”. |
||
| It is denoted by Cp. | ||
|
MATHEMATICAL EXPRESSION
|
||
| If DQp is the amount of heat is supplied at constant pressure to ‘n’ moles of a gas to increase the temperature by DT K, then | ||
|
DQp = n CpDT
|
||
|
|
||
|
OR
|
||
| heat supplied at constant pressure is consumed in two purposes: (1) To raise the temperature of gas. (2) To do work against external pressure. |
||
|
SHOW THAT CP – CV = R
|
||
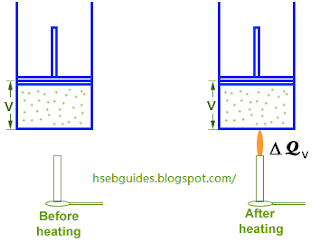
| Consider ‘n’ moles of an ideal gas contained in a cylinder fitted with a frictionless piston. If the piston is fixed and the gas is heated, its volume remains constant and all the heat supplied goes to increase the internal energy of the molecules due to which the temperature of the gas increases. If DQv is the amount of heat supplied and DT is the rise in temperature then,
DQv = n CvD T
|
||
|
The pressure of the gas increases during this process, but no work is done
because the volume is kept constant. Hence D W = 0. applying first law of thermodynamics Heat supplied = Increase in internal energy + Work done |
|
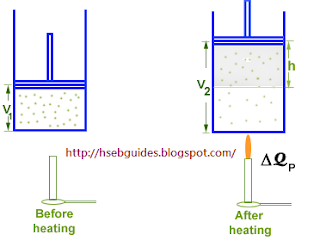
| If the piston is free to move, the gas may be allowed to expand at a constant pressure. Let the amount of heat supplied is now is DQp. The addition of heat causes two changes in the system: |
 Increase in internal energy Work done against external pressure According to the first law of thermodynamics: |
|
|
DQ = DU + DW {But DW = PDV} DQP = DU + PDV
|
|
| Since DQp = nCpDT and DU = nCvDT , therefore, |
|
|
nCpDT = nCvDT + PDV………………..(1)
|
|
| We know that PV = nRT At T1 Kelvin: PV1 = nRT1 …..(a) At T2 Kelvin: PV2 = nRT2…..(b) Subtracting (a) from (b) PV2 – PV1= nRT2 – nRT1 P(V2 – V1)= nR(T2 – T1) {(V2 – V1) = DV and (T2 – T1) = DT } PDV = nRDT |
|
|
Putting the value of PDV in equation (1)
|
|
|
nCpDT = nCvDT + nRDT nCpDT = nDT(Cv + R)Cp = (Cv + R)Cp – Cv = R
|
|