Multiplication of a vector by scalar
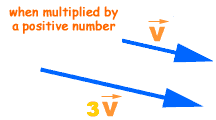
When a vector is multiplied by a positive number (for example 2, 3 ,5, 60 unit etc.) or a scalar only its magnitude is changed but its direction remains the same as that of the original vector.
If however a vector is multiplied by a negative number (for example -2, -3 ,-5, -60 unit etc.) or a scalar not only its magnitude is changed but its direction also reversed.
Division of a vector by a scalar




Top comments (0)