Any object that is given an initial velocity and the object subsequently follows a path determined by the gravitational force acting on it and by the frictional resistance of the atmosphere is called a projectile.
EXAMPLES OF PROJECTILES:
A missile shot from a gun A bomb released from a bomber Kicked or thrown balls Jumping of animals Object thrown from a window are some examples of projectile.
PROJECTILE TRAJECTORY
The path followed by a projectile is called it’s trajectory. Trajectory of a projectile is a parabola.
PROJECTILE MOTION
When a body is projected in a vertical plane making some angle with the horizontal, the motion of such a body is called as projectile motion.
In projectile motion there are two components of motion or velocity i.e. vertical component and horizontal component.
ASSUMPTIONS FOR PROJECTILE MOTION
To analyze projectile motion following three assumptions are made. The acceleration due to gravity is constant over the range of motion and is directed downward. The medium of projectile motion is assumed to be non-resistive (i.e. air resistance is negligible). The rotation of earth does not affected the motion.
ANALYSIS OF PROJECTILE MOTION
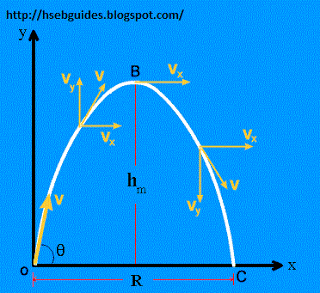
Suppose a ball is projected towards the sky (in XY-plane) with an initial velocity Vo in a direction making an angle q with the horizontal. To study the motion of the ball, it is convenient to resolve the velocity of the projectile along x and y plane. These components are Vocosq and Vosinq .
As the ball starts moving, it is subjected to a vertically downward force due to gravity. This causes a retardation in the motion of the ball along y-plane. However, there is no force acting on it along horizontal direction. Hence, the horizontal component of velocity (Vocosq) remains constant throughout its flight. The retardation along vertical direction continues till the body reaches to point B, the highest point on its trajectory. At this point the vertical component of velocity is reduced to zero and the body momentarily moves along horizontal direction with a velocity Vocosq. Beyond point B, there is an acceleration due to gravity along the vertically downward direction. Hence, the vertical component of the velocity gradually increases in the downward direction until the body strikes the ground at point ‘C’ and instead of a straight line the trajectory of projectile becomes curved.
Another correct result is that the body strikes the ground at point ‘C’ with its initial velocity, Vo again making the same angle q with the horizontal direction.
A missile shot from a gun
The acceleration due to gravity is constant over the range of motion and is directed downward.