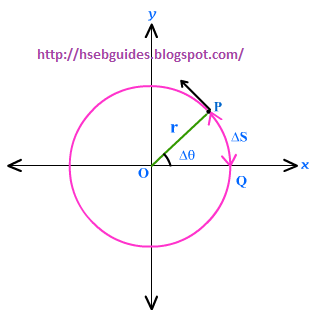
Consider a particle “P” in an object (in XY-plane) moving along a circular path of radius “r” about an axis through “O” , perpendicular to plane of the figure i.e. z-axis. Suppose the particles moves through an angle Dq in time Dt sec.
If DS is its distance for rotating through angle Dq then,
Dq = DS / r
Dividing both sides by Dt, we get Dq / Dt = (DS / r. Dt)
r Dq / Dt = DS/Dt
If time interval Dt is very small , then the angle through which the particle moves is also very
small and therefore the ratio Dq /Dt gives the instantaneous angular speed wins.
i.e.
V = rw
Tangential velocity
If a particle “P” is moving in a circle of radius “r”, then its linear velocity at any instant is equal to
tangential velocity which is :
V = rw
Tangential acceleration
Suppose an object rotating about a fixed axis changes its angular velocity by Dw in time Dt sec,
then the change in tangential velocity DVt at the end of this interval will be
DVt = r D w
Change in velocity in unit time is given by:
DV / Dt = r. Dw / Dt
if Dt approaches to zero then DV/Dt will be instantaneous tangential acceleration and Dw/Dt
will be instantaneous angular acceleration “a “.
at = ra



Top comments (0)