show that the Average translational kinetic energy of the molecules of a gas is directly proportional to absolute temperature.
Proof
According to the kinetic equation of pressure of a gas:
But r = density of gas
r = density of gas = mass of gas / volume of gas
r = density of gas = mN / V
Putting the value of density (r)
But PV = nRT
putting the value of PV, we get,
Since
number of mole (n) = molecules/Avogadro’s number
number of mole (n) = N/NA
Therefore,
But NA R = Boltzman’s constant (K), thus
Multiplying both sides by 1/2






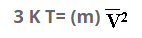
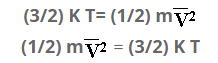



Top comments (0)