Time period
Time taken to complete one revolution or cycle is called time period denoted by “T”.
If angular velocity of a body moving in circle is w then time to complete one revolution will be
T = angular displacement / angular velocity
Angular displacement in one cycle is 2p
T = 2p / w
Centripetal acceleration
If an object is moving in a circle with constant speed, then direction of its motion is continuously changing. Due to change in direction of body an acceleration is produced in the object The direction of acceleration is towards the center of circle. This acceleration is called “centripetal acceleration”.
It is denoted by ac.
Magnitude of ac
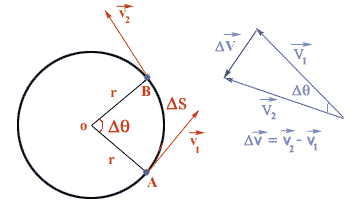
Suppose a body is moving in a circle of radius r with constant speed V. Let it travels from point A to B
in a time interval of Dt sec and covers a distance DS meter. Let velocity vector of the body at point
A be V1 and at point B be V2. Angle traced at the center during this interval Dt sec is say Dq .
Take a point O outside circle, draw velocity vector OP and OQ equal and parallel to V1 and V2. Join PQ from vector addition head and tail rule OQ i.e. V2 is resultant of OP = V1 and PQ = DV. It means PQ is the change in velocity DV during interval Dt sec.
DV = V2 – V1
angle POQ is equal to angle at the center of circle becomes V1 and V2 are perpendicular to radius lines at A and B. From geometry DACB and DOPQ are similar because both are in closed triangles and Dq are same
By similar triangles properties
D V / V = D S / r
D V = V. D S/r
Dividing both sides by D t
D V / D t = V/r . D S/D t
When Dt is very small D tè 0
D V / D t is lim DV / Dt
D tè 0
V / r lim DS / Dt
D tè 0
ac = V / r * V
ac = V2 / r
This gives the magnitude of centripetal acceleration. Since direction of change of velocity is towards center, therefore direction of ac will be towards center.
We know that
V = rw
ac = r2w 2 / r
ac = rw 2 ——– (1)
But w = 2p / T, putting the value of w
ac = r ( 2p /T)2
ac = 4p 2r / T2


Top comments (0)