ΔG, ΔH and ΔS is related by Gibb’s – He/mhottz equation as,
ΔG = ΔH – ΔS
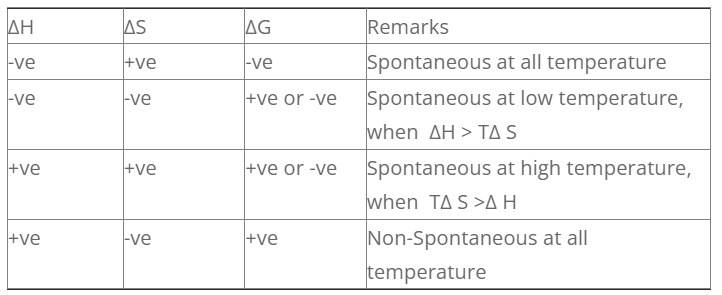
The conditions under which different process are spontaneous is discussed as follows.
1. Exothermic reaction with increase in entropy
For exothermic reaction, ΔH = -ve
For increase in entropy, ΔS = +ve
For such process, the sign of G is always negative. So such process are spontaneous at all temperature.
2. Exothermic reaction with decrease in entropy
For exothermic reaction, ΔH = -ve
For decrease in entropy, ΔS = -ve
For such process, the value of S can be +ve or -ve. So the process is spontaneous at low temperature when H > TΔS.
3. Endothermic reaction with increase in entropy
For endothermic r× n, Δ H = +ve
For increase in entropy, ΔS = +ve
For such process, the value of G can be +ve or -ve. The process is spontaneous at high temperature when, TΔS > H.
4. Endothermic reaction with decrease in entropy
For endothermic r× n, ΔH = +ve
For increase in entropy, ΔS = -ve
For such process, the value of G is always positive. So, this type of process is non-spontaneous at all temperature.
Numerical
For a process the change in enthalpy and entropy is 40.82 KJ mole-1 and 109.4 JK-1 mole-1 respectively will the process be spontaneous at 500c.
Soln Given,
Δ S = 109.4 JK-1mol-1
ΔH = 40.82 KJ mol-1 × 1000J
= 40820 Jmol-1
ΔG = ΔH – T Δ S
= 40820 – 323 × 109.4
For a chemical reaction,
2 Ag2O (s) 4 Ag (s) + O2 (g). H = 61.2 KJmol-1
Calculate the temperature above which the reaction is spontaneous.
Here,
ΔH° = 61.2 × 1000 Jmol-1 = 61200 Jmol-1
ΔS° = 132 JK-1mol-1
TΔ S >Δ H°
T > 61200/132
T > 463.63K


Top comments (0)