For the reaction,
2NO + Cl2 → 2NOCl
Following datas were obtained:
Determine the order of the reaction with respect to NO, Cl2 and overall order. Write the rate law expression and determine the value of rate constant.
Soln:
Let the order w.r.t. NO and Cl2 be in and n. The rate low expression will be,
Dividing eqn (ii) by (i) we get,
Dividing eqn (iii) by (ii), we get,
order w.r.t. NO = 2
order w.r.t. Cl2 = 1
Overall order of r × n = 2 + 1 = 3
Then, the rate law expression,
Rate = k [NO]2 [Cl2]
Putting the value of m and n in equation (i), we get,
The experimental data for the reaction
Determine the order of the r × n wrt A and B and overall r × n. Write the rate law expression and determine the value of rate of constant.
Solution:
Let the order w.r.t. A and B be m and n. The rate law expression will be,
Dividing eqn (ii) by (i) we get,



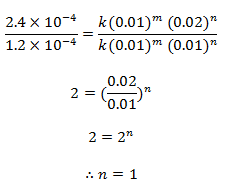
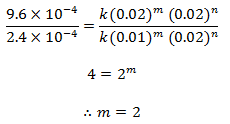
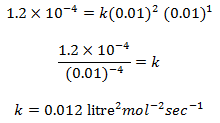


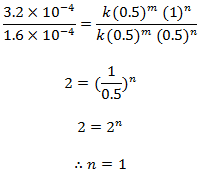
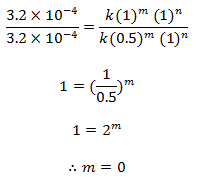


Top comments (0)