Elastic collision
An elastic collision is that in which the momentum of the system as well as kinetic energy of the system before and after collision is conserved.
Inelastic collision
An inelastic collision is that in which the momentum of the system before and after collision is conserved but the kinetic energy before and after collision is not conserved.
Elastic collision in one dimension
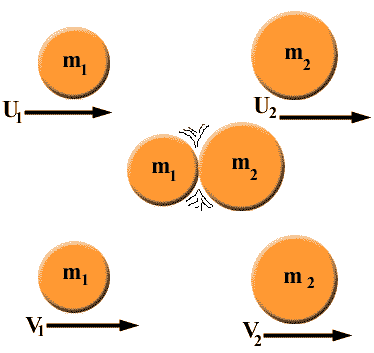
Consider two non-rotating spheres of mass m1 and m2 moving initially along the line joining their centers with velocities u1 and u2 in the same direction. Let u1 is greater than u2. They collide with one another and after having an elastic collision start moving with velocities v1 and v2 in the same directions on the same line.
Momentum of the system before collision = m1u1 + m2u2
Momentum of the system after collision = m1v1 + m2v2
According to the law of conservation of momentum:
m1u1 + m2u2 = m1v1 + m2v2
m1v1 – m1u1 = m2u2 – m2v2
m1(v1 – u1) = m2(u2 – v2) ——-(1)
Similarly
K.E of the system before collision = ½ m1u12 + ½ m2u22
K.E of the system after collision = ½ m1v12 + ½ m2v22
Since the collision is elastic, so the K.E of the system before and after collision is conserved .
Thus
½ m1v12 + ½ m2v22 = ½ m1u12 + ½ m2u22
½ (m1v12 + m2v22) = ½ (m1u12 + ½ m2u22
m1v12-m1u12=m2u22-m2v22
m1(v12-u12) = m2(u22-v22)
m1(v1+u1) (v1-u1) = m2(u2+v2) (u2-v2) ——- (2)
Dividing equation (2) by equation (1)
V1+U1 = U2+V2
From the above equation
V1=U2 +V2 -U1_________(a)
V2=V1+U1 -U2_________(b)
Putting the value of V2 in equation (1)
m1 (v1-u1) =m2 (u2-v2)
m1 (v1-u1) =m2{u2-(v1+u1-u2)}
m1(v1-u1)=m2{u2-v1-u1+u2}
m1(v1-u1)=m2{2u2-v1-u1}
m1v1-m1u1=2m2u2-m2v1-m2u1
m1v1+m2v1=m1u1-m2u1+2m2u2
v1(m1+m2)=(m1-m2)u1-2m2u2
In order to obtain V2 putting the value of V1 from equation (a) in equation (i)
m1 (v1-u1) = m2(u2-v2)
m1(u2+v2-u1-u1)=m2(u2-v2)
m1(u2+v2-2u1)=m2(u2-v2)
m1u2+m1v2-2m1u1=m2u2-m2v2
m1v2+m2v2=2m1u1+m2u2-m1u2
v2(m1+m2)=2m1u1+(m2-m1)u2

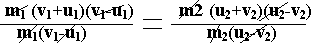
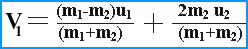
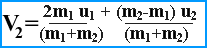

Top comments (0)