Half Life of a reaction is time required to reduce the initial concentration to half. The half-life of a reaction depends on the order of reaction. The variation of half-life with order is given as:
Integrated rate law expression
For Zeroth order reaction
For first order reaction
Integrating on both sides, we get,
So, half-life of first order reaction is independent of initial concentration.
Numerical
The half-life of a first order reaction is 50 mins. Calculate the time required to complete 75% of the reaction.
Given,
Again,
initial concentration (a) = 100 (let) then
at time t,
Concentration left (a-x) = 100-75 = 25
We have,
Calculate the half period of first order reaction when rate constant is 5 year-1.
We have,
For 1st order reaction
t1/2 = 0.693/5
= 0.1386 year



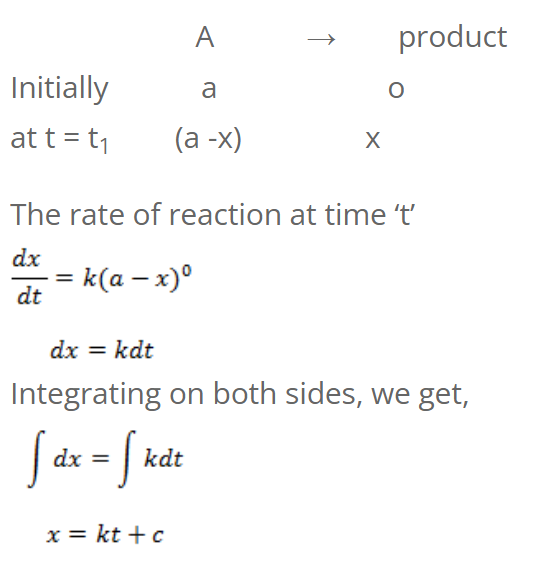
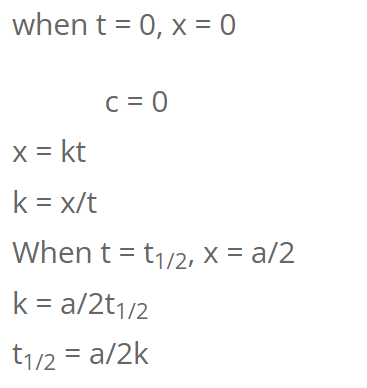
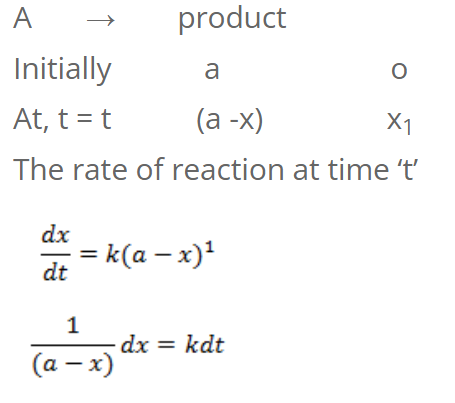
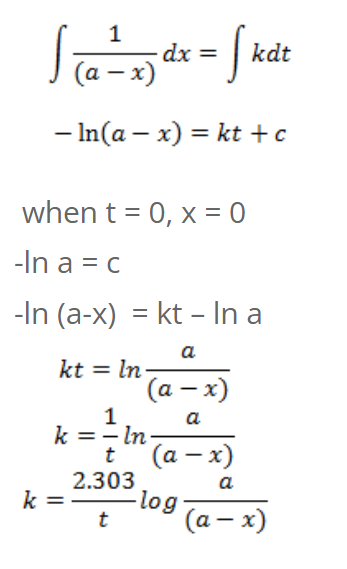
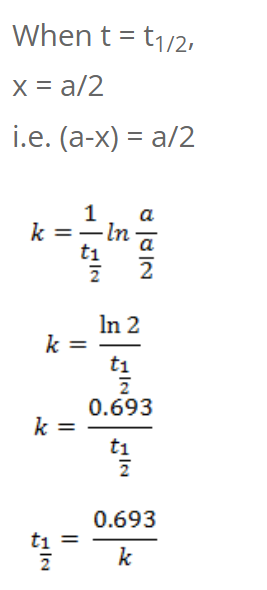
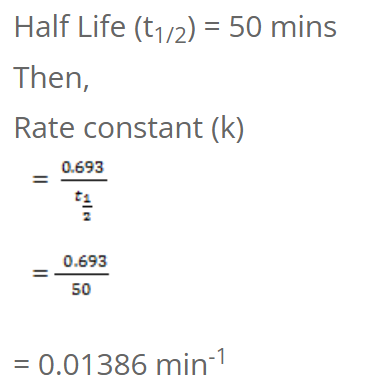
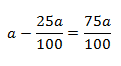
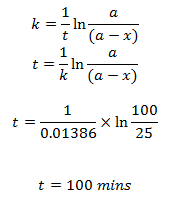

Top comments (0)