The Laws of returns to scale

The law of returns scale describes about the long run production phenomenon. In the long run all the factors of production are changeable. So, this law explains the rate of change in output due to the same proportionate change in input i.e. labor and capital. According to this theory production process may have three kinds of returns to scale.

1. Increasing returns to scale (IRS):

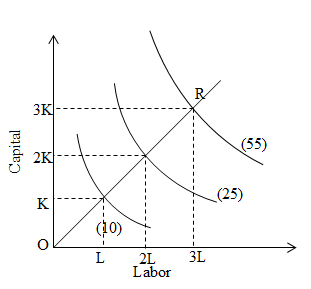
If the proportionate change in output is more than the proportionate change in inputs is known as IRS. For example if the output is change by more than double due to doubling of the inputs i.e. capital and labor. We can explain it by the help of following figure:

Reasons behind IRS:

i. Technical managerial indivisibility.
ii. Higher degree of specialization.
iii. Dimensional relation

2. On the given figure, x and y-axis represent labor and capital respectively. When 1 unit of C and L are used total production is 10 units. If we double input then output is 25. If we triple input then output is 55. Hence, proportionate change in output is less than that in input.

3. Decreasing returns to scale (DRS):
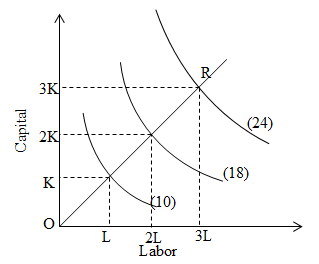
If the proportionate change in output is less than the proportionate change in inputs i.e. labor and capital is known as DRS. For example proportionate change in output is less than double due to doubling the inputs. We can describe it with the help given figure:

When the 1st unit of L and C are used total output is 10 units. When L and C is increased by doubling then output is 18 and if they are tippled then output is 24. Hence, proportionate change in output is less than change in input.

4. Constant returns to scale (CRS):

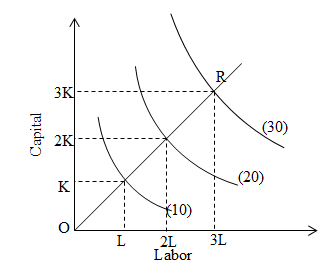
If the proportionate change in input and output are equal it is known as CRS. For example the proportionate change in output is equal to proportionate change in input. We can explain it with figure:

On the above figure, when 1st unit if input are used total output is 1o0 units. When inputs are doubled then output is 20 units and when input are tripled then output is 30 units. Hence, proportionate change in input is equal to that change in output.